Model-Free (Isoconvertional) Analysis Methods in Kinetics Neo
There is no assumption of the reaction type. Limited usage.
Introduction
Model-free analysis allows for determination of the activation energy of a reaction process without assuming a kinetic model for the process. Also, the reaction type is usually not required to calculate the activation energy. However, it is not possible to determine the number of reaction steps, their contribution to the total effect or the order in which they occur.
Assumptions of Model-Free Analysis
Model-free analysis is based on two assumptions:
1. The reaction can be described by only one kinetic equation for the degree of reaction α:
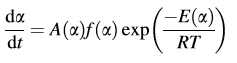
where E(α) is the activation energy depending on the conversion α, and A(α) is the pre-exponential factor.
Activation energy E of chemical reaction is calculated without any assumption about reaction type, but pre-exponential factor A can be found only under assumption about reaction type.
2. The reaction rate at a constant value of conversion is only a function of temperature.
Results of Model-Free Analysis
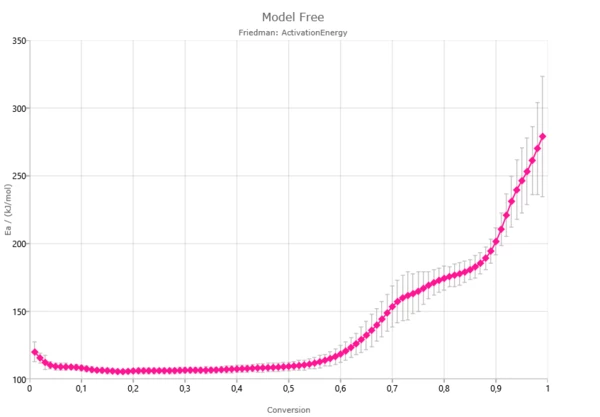
Some model-free methods calculate single values of E and A, another model-free methods calculate dependences of activation energy E(α) and pre-exponential factor A(α) as the function of degree of conversion α.
Model-Free Methods in Kinetics Neo
In Kinetics Neo, the following groups of methods can be used:
1. Single-value model-free methods, where one value of E and A are found:
- ASTM E698,
- ASTM E2890,
- ASTM E1641,
- Isothermal Arrhenius for time-to-event,
- Dynamic Arrhenius for failure temperature (ASTM E2070D),
- ASTM E2070(A) for isothermal data.
2. Multiple-value model-free methods, where dependences E(α) and A(α) are found:
- Friedman,
- Ozawa-Flynn-Wall (OFW),
- Kissinger-Akahira-Sunose (KAS),
- Vyazovkin,
- Numerical Optimization (Kinetics Neo only).
Advantages and Disadvantages of Model-Free Methods
The Friedmananalysis is an isoconversional method whereas the Ozawa-Flynn-Wall (OFW), Kissinger-Akahira-Sunose (KAS) and Vazovkin methods analyses are integral isoconversional methods. In all methods, the measurements are analyzed for multiple conversion levels. Friedmanrequires at least two measurements.
In addition to three dynamic measurements, OFW, KASand Vyazovkin for heating require positive heating rates.
The Numerical Optimization uses digital simulation in determining the activation energy and pre-exponential factor to achieve the best agreement between simulated and experimental curves. At least two measurements are required.
In all of the methods, the activation energy is determined using the points at the same conversion (0.01, 0.02, …, 0.99) from the measurements at different heating rates or under different isothermal conditions (for Friedmanand Numerical Optimization).
| Model-Free Methods | Advantage | Disadvantage |
|---|---|---|
| Methods based on a single conversion | ||
| • ASTM E698 • ASTM E1641 • ASTM E2890 • Isothermal Arrhenius • Dynamic Arrhenius | • Only for one-step reactions; for complex reactions, the points are not on a straight line. • ASTM: Only for dynamic measurements. • Only one point is evaluated; all other information is not used. | |
| Conversion-dependent methods | ||
| ASTM E2070(A) | • For multiple-step reactions without parallel reaction steps. • Evaluation of each reaction point. • Suitable for isothermal measurements only. | For parallel and independent reactions, the mean values of Ea are given. |
| Friedman | • For multiple-step reactions without parallel reaction steps. • Evaluation of each reaction point. • Suitable for dynamic and isothermal measurements. | For parallel and independent reactions, the mean values of Ea are given. |
| Ozawa-Flynn- Wall (OFW) | • For multiple-step reactions without parallel reaction steps. • Evaluation of each reaction point. | • Suitable only for dynamic runs. • For parallel and independent reactions, the mean values of Ea are given. |
| Kissinger-Akahira-Sunose (KAS) | • For multiple-step reactions without parallel reaction steps. • Evaluation of each reaction point. | • Suitable only for dynamic runs. • For parallel and independent reactions, the mean values of Ea are given. |
| Vyazovkin for Heating | • For multiple-step reactions without parallel reaction steps. • Evaluation of each reaction point. | • Suitable only for dynamic runs. • For parallel and independent reactions, the mean values of Ea are given. |
| Numerical Optimization | • For multiple-step reactions without parallel reaction steps. • Evaluation of each reaction point. • Suitable for dynamic and isothermal. measurements | • For parallel and independent reactions, the mean values of Ea are given. |
Model-Free Graphs in Kinetics Neo
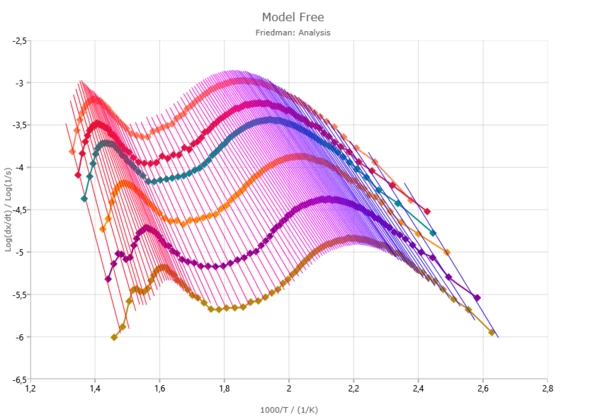
- Analysis graph with Y-axis:
- log (heating rate),
- log (heating rate/T2),
- log dx/dt versus 1000/T,
- log(time) versus 1000/T;
- Plots of activation energy and pre-exponential factor vs. conversion;
- Master plot for f(α);
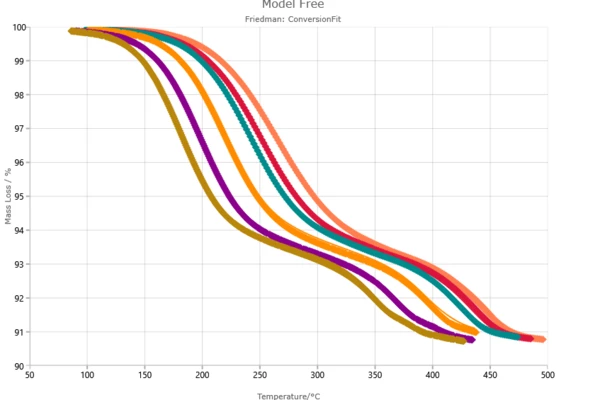
- Conversion fit.
