Features
Curing Reactions with Diffusion Control
(Kinetics Neo Project Type "DSC Curing" only)
The kinetic reaction sometimes is additionally complicated by the fact that for some conditions (low heating rates, annealing periods) the glass temperature of the polymer increases faster than the sample temperature. After the partial or complete freezing of the reaction mixture, the reaction is no longer controlled by the kinetics of the chemical reaction, but by diffusion processes.
If diffusion hindrances must be considered, the Rabinowitch equation (1) can be used for calculation of the entire rate constant k:
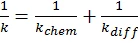
where kchem is the chemical reaction rate:
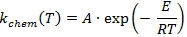
and kdiff is the diffusion rate.
The form of the temperature function of kdiff is the modified equation of WLF type.
For temperatures above the glass temperature Tg (T >= Tg), Kinetics Neo uses equation (3a):
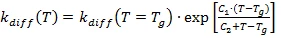
Below the glass transition, the temperature dependence is according to Arrhenius (3b):
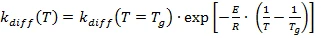
with
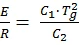
At T = Tg, both formulas (3a) and (3b) are going continuously from one to another range up to the first derivative.
If in model definition a reaction step is defined with diffusion control (via checkbox), then additional parameters must be optimized for each step with diffusion control:
Log(kdiff) at T = Tg and
C1 and C2 as global parameters of the mixture under investigation.
Related Literature
[1] H.J. Flammersheim, J. Opfermann, Formal kinetic evaluation of reactions with partial diffusion control, Thermochemica Acta 337 (1999), 141-148
[2] G. Van Assche, S. Swier, B. Van Mele, Modeling and experimental verification of the kinetics of reaction polymer systems, Thermochemica Acta 388 (2002), 327-341
