How Kamal-Sourour parameters in Kinetics Neo correspond to original equation da/dt=(k1+k2*a^m)*(1-a)^n?

Kamal-Sourour model in the literature [1] is developed for curing of epoxy at isothermal conditions and therefore does not contain the temperature dependence for the rate constants:

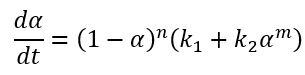
In Kinetics Neo we use extended, improved version of equation, where the reaction rates have the Arrhenius dependence on temperature:

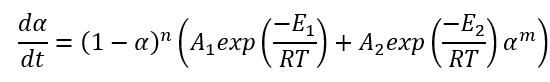
If the pre-exponential factor A₁ is placed outside of brackets, then the equation looks as following:

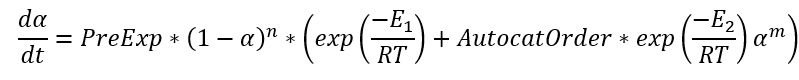
where PreExp = A₁, AutocatOrder = A₂/A₁

For reaction A→B the reactant A has concentration a (changes from 1 to 0 during reaction), and the product B has concentration b (changes from 0 to 1). Degree of conversion alpha corresponds to concentration b of product B, and (1- alpha) corresponds to concentration a of reactant A. After this replacement the kinetic equation is rewritten using concentrations (here is example for step A→B):

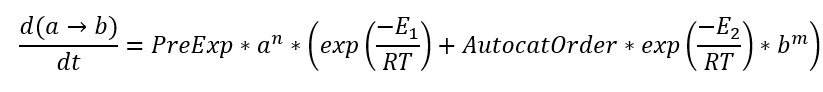
This equation is equal to equation in Kinetics Neo:

d(a->b)/dt=PreExp*a^n* [Exp(-ActivationEnergy/(RT)) +AutocatOrder*(b^m)*Exp(-ActEnergy2/(RT))]

where ActivationEnergy = E₁, and ActEnergy2=E₂.

For isothermal conditions this equation is equal to classical Kamal-Sourour equation:

dα/dt=(k₁+k₂*α^m)*(1-α)ⁿ  with k₁= PreExp* Exp(-ActivationEnergy/(RT)) and k₂= PreExp* AutocatOrder *Exp(-ActivationEnergy/(RT))

Simplified Kamal-Sourour models in Kinetics Neo:

Cmn is the simplified Kamal-Sourour reaction, where E₁=E₂

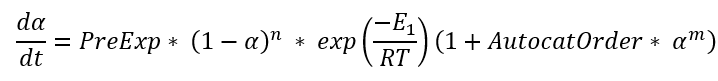
Cn is the simplified Kamal-Sourour reaction, where E₁=E₂and m=1

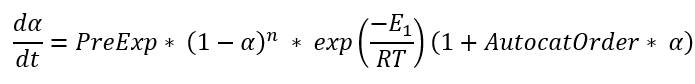
C1 is the simplified Kamal-Sourour reaction, where E₁=E₂ m=1 and n=1 

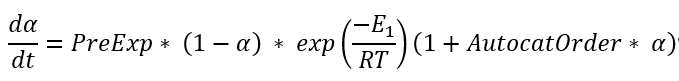
Referencees

1.       S.Sourour, M.R.Kamal Differential Scanning Calorimetry of Epoxy Cure: Isothermal Cure Kinetics, Thermochimica Acta, 14 (1976) 41-59.